Two wires of the same material (Young's modulus $Y$ ) and same length $L$ but radii $R$ and $2R$ respectively are joined end to end and a weight $W$ is suspended from the combination as shown in the figure. The elastic potential energy in the system is
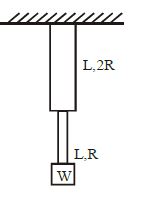
Two wires of the same material (Young's modulus $Y$ ) and same length $L$ but radii $R$ and $2R$ respectively are joined end to end and a weight $W$ is suspended from the combination as shown in the figure. The elastic potential energy in the system is

- A
$\frac{{3{W^2}L}}{{4\pi {R^2}Y}}$
- B
$\frac{{3{W^2}L}}{{8\pi {R^2}Y}}$
- C
$\frac{{5{W^2}L}}{{8\pi {R^2}Y}}$
- D
$\frac{{{W^2}L}}{{\pi {R^2}Y}}$
Similar Questions
If the force constant of a wire is $K,$ the work done in increasing the length of the wire by $l$ is
If the force constant of a wire is $K,$ the work done in increasing the length of the wire by $l$ is
A uniform metal rod of $2\,\,mm^2$ cross section fixed between two walls is heated from $0\,^oC$ to $20\,^oC$ . The coefficient of linear expansion of rod is $12\,\,\times\,\,10^{-6}\,/^oC$ . Its Young's modulus of elasticity is $10^{11}\,\,N/m^2$ . The energy stored per unit volume of rod will be ....... $J/m^3$
A uniform metal rod of $2\,\,mm^2$ cross section fixed between two walls is heated from $0\,^oC$ to $20\,^oC$ . The coefficient of linear expansion of rod is $12\,\,\times\,\,10^{-6}\,/^oC$ . Its Young's modulus of elasticity is $10^{11}\,\,N/m^2$ . The energy stored per unit volume of rod will be ....... $J/m^3$
A wire suspended vertically from one end is stretched by attaching a weight $200 \,N$ to the lower end. The weight stretches the wire by $1 \,mm$. The elastic potential energy gained by the wire is ....... $J$
A wire suspended vertically from one end is stretched by attaching a weight $200 \,N$ to the lower end. The weight stretches the wire by $1 \,mm$. The elastic potential energy gained by the wire is ....... $J$
An Indian rubber cord $L$ metre long and area of cross-section $A$ $metr{e^2}$ is suspended vertically. Density of rubber is $D$ $kg/metr{e^3}$ and Young's modulus of rubber is $E$ $newton/metr{e^2}$. If the wire extends by $l$ metre under its own weight, then extension $l$ is
An Indian rubber cord $L$ metre long and area of cross-section $A$ $metr{e^2}$ is suspended vertically. Density of rubber is $D$ $kg/metr{e^3}$ and Young's modulus of rubber is $E$ $newton/metr{e^2}$. If the wire extends by $l$ metre under its own weight, then extension $l$ is
On stretching a wire, the elastic energy stored per unit volume is
On stretching a wire, the elastic energy stored per unit volume is
